BARISAN, DERET, DAN BENTUK AKAR
Pendahuluan Barisan dan Deret
Susunan bilangan yang dipisahkan dengan tanda koma disebut barisan.
Contoh: 2, 4, 6, 8, 10, ... dan 1, 3, 5, 7, 9, ...
Suku-suku suatu barisan dapat didefinisikan dengan suatu rumus suku ke-n.
Contoh:
yang akan menghasilkan
dan ditulis 5, 7, 9, 11, ...Sebuah definisi induktif untuk suatu barisan diberikan dengan menyatakan suku pertama dan aturan yang menunjukkan bagaimana memperoleh suku berikutnya berdasarkan suku sebelumnya.
Contoh:
yang akan menghasilkan barisan bilangan 1, 5, 13, 29, ...
Barisan dan Deret Aritmatika
Barisan aritmatika: a, a + b, a + 2b, ... merupakan barisan yang memiliki beda sama.
Contoh: 4, 6, 8, 10, 12, ... dengan beda 2.
Suku ke-n barisan aritmatika
ditentukan dengan rumus:
dengan a = suku pertama, b = beda, dan n = banyak suku.
Deret Aritmatika
Jika suku-suku dari barisan aritmatika dijumlahkan maka akan membentuk deret aritmatika.
Contoh: 2 + 3 + 4 + 5 + 6 + ...
Jumlah n suku pertama suatu deret aritmatika dinyatakan dengan rumus:
dengan a = suku pertama, b = beda, n = banyak suku.
Barisan Geometri
Contoh: 2, 6, 18, 54, 162, ... dengan rasio 3.
Untuk menemukan suku ke-n barisan geometri digunakan rumus:
dengan a = suku pertama, r = rasio, n = banyak suku.
Deret Geometri
Jumlah n suku pertama suatu deret geometri ditentukan dengan rumus:
dengan a = suku pertama, r = rasio.
Jumlah deret geometri tak hingga ditentukan dengan rumus:
Bentuk Akar
Dalam matematika, akar positif dari bilangan x ditulis:
Sebuah bilangan yang dapat dinyatakan dalam bentuk:
dengan a dan b bilangan bulat, disebut bilangan rasional.
Contoh:
Sebuah bilangan irasional adalah bilangan yang tidak dapat dinyatakan dalam bentuk tersebut.
Contoh:
Bilangan-bilangan seperti:
dinamakan bentuk akar.
Kita gunakan bentuk akar apabila kita ingin menyatakan secara tepat.
Menyederhanakan Bentuk Akar
Perhatikan bentuk:
dan
Secara umum, dapat tunjukkan bahwa:
Dengan cara yang sama kita peroleh:
Contoh:
Tetapi
dan
Menyederhanakan Hasil Kali yang Memuat Bentuk Akar
Perhatikan bentuk berikut.
Pasangan bilangan seperti
disebut pasangan sekawan.
Untuk menyederhanakan bentuk seperti:
dilakukan dengan cara mengalikan pembilang dan penyebut dengan bentuk sekawan dari penyebutnya, yaitu:
Sehingga diperoleh bentuk sederhana seperti berikut.
Topik Lainnya:
1. Vektor2. Lingkaran dan Koordinat Geometri
3. Aljabar dan Grafik
4. Trigonometri
5. Kalkulus













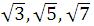

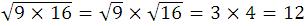









Tidak ada komentar:
Posting Komentar