ALJABAR DAN GRAFIK
Polinomial dan Persamaan
Suatu fungsi polinomial p(x) bukan merupakan sebuah persamaan.
Sebuah persamaan menyatakan kesamaan, terutama dengan nol dan harus memuat tanda =.
Fungsi Kuadrat
Bentuk umum fungsi ini adalah:
Terdapat 3 cara utama untuk menyelesaikan persamaan kuadrat, yaitu pemfaktoran, menggunakan rumus, dan melengkapkan kuadrat.
Pemfaktoran (selalu coba cara ini dulu)
Untuk menyelesaikan persamaan kuadrat:
mula-mula kita faktorkan suku-suku di ruas kiri sehingga diperoleh:
Menggunakan Rumus
Penyelesaian persamaan kuadrat dapat juga diselesaikan dengan rumus (selanjutnya biasa disebut rumus abc), sebagai berikut.
Bentuk
1) Jika D = 0, maka terdapat tepat satu penyelesaian riel.
2) Jika D > 0, maka terdapat dua penyelesaian riel berbeda.
3) Jika D < 0, maka tidak terdapat penyelesaian riel.
Dalam kasus D < 0 (persamaan kuadrat tidak mempunyai penyelesaian riel), penyelesaiannya merupakan bilangan kompleks, yaitu bilangan yang memuat
dan biasa dinyatakan dengan huruf i.
Melengkapkan Kuadrat
Untuk menyelesaikan persamaan kuadrat:
dengan menggunakan cara ini kita lakukan langkah-langkah seperti berikut.
Grafik Fungsi Kuadrat
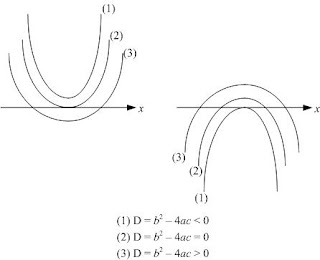
Bentuk grafik fungsi kuadrat:
bergantung pada nilai a dan D (diskriminan).
Berikut ini kemungkinan bentuk grafik fungsi tersebut.
Grafik dari beberapa fungsi lainnya diperlihatkan pada gambar di bawah.
Transformasi Dasar
Apabila grafik suatu fungsi f(x) diketahui, maka kita dapat menggambar grafik fungsi lain seperti f(x + a), f(x - a), f(x) + b, f(x) - b, kf(x), dan f(kx) dengan menggunakan transformasi (translasi/geseran) berdasarkan grafik fungsi f(x).
Berikut ini diperlihatkan grafik suatu fungsi f(x) beserta grafik-grafik lainnya yang diperoleh dengan transformasi.
.JPG)
+b.JPG)
.JPG)
Polinomial
Suatu fungsi polinomial f(x) dibentuk dengan menjumlahkan suku-suku yang hanya memuat pangkat bulat positif dari x, mungkin juga dengan sebuah konstanta. (catatan: suatu polinomial boleh hanya memuat 0).
Contoh:
Secara umum, polinomial dapat dinyatakan dalam bentuk:
dengan
Derajat suatu polinomial adalah nilai dari pangkat terbesar x.
Polinomial berderajat 1 disebut linier, berderajat 2 disebut kuadrat, berderajat 3 disebut kubik, dan berderajat 4 disebut kuartik.
Pemfaktoran dan Penjabaran
Pemfaktoran
Berikut ini disajikan 3 bentuk pemfaktoran yang penting.
Penjabaran
Beberapa bentuk penjabaran penting disajikan berikut ini.
Teorema Faktor dan Teorema Sisa
Teorema Faktor
Untuk polinomial p(x), jika p(a) = 0 maka (x - a) adalah sebuah faktor dari p(x).
Sebaliknya, jika (x - a) adalah sebuah faktor dari p(x) maka p(a) = 0.
Teorema Sisa
Jika polinomial p(x) dibagi (x - a), maka sisanya adalah p(a).
Pecahan Parsial
Untuk pecahan murni:
dengan P dan Q adalah polinomial dengan derajat P kurang dari derajat Q:
Sebuah faktor linier ax + b pada penyebut akan menghasilkan pecahan parsial berbentuk:
Faktor linier berbentuk:
pada penyebut akan menghasilkan pecahan parsial berbentuk:
Faktor kuadrat:
pada penyebut akan menghasilkan pecahan parsial berbentuk:
Pecahan tak murni memerlukan penjumlahan suku. Ini adalah polinomial berderajat n - d dengan n adalah derajat pembilang dan d adalah derajat penyebut.
Pertidaksamaan
Berikut disajikan beberapa bentuk pertidaksamaan dasar beserta artinya.
Teorema Binomial
Perhatikan pola bilangan Segitiga Pascal berikut.
Ingat bahwa bilangan-bilangan pada baris Segitiga Pascal merupakan koefisien pada penjabaran bentuk:
Beberapa contoh penjabaran bentuk itu adalah sebagai berikut.
Kombinasi
Kombinasi adalah banyak cara membuat pilihan r objek dari sekumpulan n objek berbeda apabila urutan pilihan tidak dipertimbangkan.
Kombinasi seperti tersebut ditulis dengan simbol:
dan ditentukan dengan rumus:
Faktorial
Untuk setiap n bulat positif, faktorial didefinisikan sebagai berikut:
Teorema Binomial
Jika n bilangan bulat positif, maka berlaku:
Deret Binomial
Jika n bilangan bulat positif dan nilai mutlak x kurang dari 1, maka:
Pangkat dan Logaritma
Rumus operasi bilangan berpangkat
Logaritma
Untuk setiap bilangan bulat positif b (b tidak sama dengan 1), berlaku:
Rumus perubahan basis
Logaritma dengan basis 10 biasanya cukup ditulis dengan log (tanpa ditulis basisnya).
Contoh:
Logaritma dengan basis e (bilangan mendekati 2,718) biasa ditulis ln (logaritma natural).
Menyelesaikan Persamaan dengan Pangkat tidak diketahui
Untuk menyelesaikan persamaan:
dilakukan dengan cara mengambil logaritma dari kedua ruas, sehingga diperoleh:
Topik lainnya:
2. Lingkaran dan Koordinat Geometri
3. Barisan, Deret, dan Bentuk Akar
4. Trigonometri
5. Kalkulus
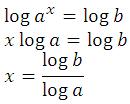
Tidak ada komentar:
Posting Komentar