RUMUS DASAR MATEMATIKA 6

KALKULUS

Beberapa Fungsi dan Turunannya

Aturan Rantai pada Turunan

Aturan Perkalian

Jika y = uv dengan u dan v fungsi-fungsi dalam x, maka:

Aturan tersebut dapat dinyatakan dalam notasi fungsi seperti berikut:

Aturan Hasil Bagi

Jika y = u/v dengan u dan v fungsi-fungsi dalam x, maka:

Dalam notasi fungsi, rumus tersebut dapat dinyatakan sebagai berikut:

Titik Stasioner

Titik stasioner dari y = f(x) terjadi apabila

Jenis titik ini dapat diklasifikasikan sebagai titik maksimum lokal, minimum lokal, atau titik belok. Uji turunan kedua, yaitu:

dapat digunakan untuk menentukan jenis titik stasioner, sebagai berikut:

Gambar situasinya:

Integral Dasar

Beberapa rumus integral dasar disajikan dalam tabel berikut.

Aturan Linieritas dalam Integral

Integral Parsial

Integral Tak Tentu

Bentuk integral, seperti:

memuat konstanta bebas c, sehingga integral ini tidak memiliki nilai tunggal. Integral seperti ini disebut integral tak tentu.

Integral yang Menghasilkan Log

Luas di Bawah Kurva

Perhatikan gambar berikut.

Daerah yang diarsir dibatasi oleh garis x = a, x = b, dan kurva y = f(x). Jika L menyatakan luas daerah yang diarsir, maka:

x = a dan x = b berturut-turut disebut batas bawah dan batas atas integral.

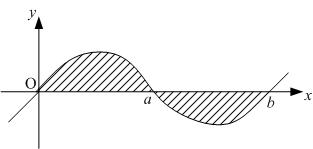
Bagaimana menentukan luas daerah yang berada di bawah sumbu x dengan menggunakan integral?

Perhatika gambar berikut.

Daerah yang diarsir dibatasi oleh kurva y = f(x) dan sumbu x. Rumus integral yang sesuai untuk menentukan luas daerah yang diarsir tersebut adalah:

Volume Benda Putar

Apabila kurva y = f(x) diputar 360 derajat mengelilingi sumbu x, volume benda putar yang terjadi dapat ditentukan dengan rumus:

Gambar situasinya:

Selanjutnya apabila kura x = g(y) diputar sejauh 360 derajat mengelilingi sumbu y, volume benda putar yang terjadi ditentukan dengan rumus sebagai berikut:

Gambar situasinya:

Persamaan Diferensial

Suatu persamaan yang memuat satu atau lebih turunan disebut persamaan diferensial.

Persamaan seperti:

dinamakan persamaan diferensial orde pertama karena memuat turunan pertama dy/dx.

Menyelesaikan Persamaan Diferensial

Persamaan diferensial orde pertama yang dapat ditulis:

dapat diselesaikan dengan cara mengubah bentuk dan mengintegralkan kedua ruasnya seperti berikut.

Contoh:

Topik lainnya:

1. Vektor
2. Lingkaran dan Koordinat Geometri
3. Barisan, Deret, dan Bentuk Akar
4. Aljabar dan Grafik
5. Trigonometri

RUMUS DASAR MATEMATIKA 5

TRIGONOMETRI

Derajat dan Radian

Besar suatu sudut biasanya dinyatakan dalam ukuran derajat atau radian. Hubungan antara keduanya adalah sebagai berikut.

Perbandingan Trigonometri dan Nilainya untuk Sudut Istimewa

Perbandingan trigonometri sudut lancip

Nilai perbandingan trigonometri sudut-sudut istimewa

Grafik Fungsi Trigonometri

Grafik fungsi sinus

Grafik fungsi cosinus

Grafik fungsi tangen

Grafik fungsi secan

Grafik fungsi cosecan

Grafik fungsi cotangen

Grafik Invers Fungsi Trigonometri

Invers fungsi sinus atau arcSin, ditulis dengan simbol

Artinya y adalah sudut yang nilai sinusnya x. Dalam hal ini x adalah bilangan riel dalam interval

dan y adalah sudut dalam satuan derajat.

Sebagai contoh,

Invers fungsi cosinus atau arcCos dan invers fungsi tangen atau arcTan berturut-turut ditulis dengan simbol

didefinisikan dengan cara serupa.

Grafik ketiga fungsi tersebut adalah sebagai berikut.

Grafik fungsi arcSin

Grafik fungsi arcCos

Grafik fungsi arcTan

Identitas Trigonometri

Identitas Sudut Negatif

Rumus Jumlah Sudut dan Identitas Sudut Rangkap

Hasil Kali Sinus atau Cosinus

Jumlah atau Selisih Sinus atau Cosinus

Mengubah Bentuk aSin x + bCosx

Untuk bilangan positif a dan b, berlaku:

Sudut-sudut Kecil

Untuk setiap sudut kecil x, dalam ukuran radian, berlaku:

Luas Segitiga

Aturan Sinus dan Cosinus

Luas Juring dan Panjang Busur Lingkaran

Luas Juring

Panjang Busur

Topik lainnya:

1. Vektor
2. Lingkaran dan Koordinat Geometri
3. Barisan, deret, dan Bentuk Akar
4. Aljabar dan Grafik
5. Kalkulus